Açısal Hızın Yönü
Düzgün çembersel hareket bir hareketlinin yörüngesinin (yani izlediği yolun) bir çember üzerinde olduğu ve çizgisel hızının büyüklüğünün (yani süratinin) sabit olduğu (yani çizgisel ivmesinin sıfır olduğu) hareket türüdür. Bir kaç yıl önceye kadar bu harekete düzgün dairesel hareket deniyordu, daire alan ifade ettiği için daha tutarlı olan, yörüngeyi yani hareketin izini işaret eden çember terimi kullanılmaya başlandı. Daha önceki konularda doğrusal hareketi öğrenmiştiniz, doğrusal harekette yörünge bir çizgiydi, şimdi ise bir çember. Bu nedenle yeni kavramlara ihtiyacımız olacak. Sırasıyla periyot, frekans, açısal hız, çizgisel hız ve merkezcil ivme kavramlarını inceleyeceğiz.
Düzgün Çembersel Hareket Temel Değişkenler nelerdir?
Periyot nedir?
Periyot bir hareketin kendisini tekrarlaması anlamına gelir. Düzgün çembersel hareket için periyot cismin hareketine başladığı noktaya tekrar dönmesi (bir devri tamamlaması) için geçen süredir. Bir başka deyişle, cisim bir tam tur atana kadar geçen zamana periyot denir. Periyot matematiksel olarak T simgesiyle gösterilir; periyodun birimi zaman birimi olan saniyedir (s).
Örneğin, aşağıda aynı yarıçaplı çember bir yörüngede hareket eden üç farklı cisim görülüyor. Bunların ilkinin (yeşilin) periyodu T = 4 s, ikincisinin (turuncunun) T = 2 s, üçüncüsünün (kırmızının) T = 1 s. Periyot azaldıkça dönme hareketinin hızlandığına dikkat edin. Kırmızı cisim turuncunun iki katı kadar hızlı dönüyor, turuncu da yeşilin iki katı hızlı dönüyor.
Frekans nedir?
Periyodun düzgün çembersel harekette bir turun kaç saniyede tamamlandığı anlamına geldiğini biliyoruz. Frekans da bir saniyede kaç tur tamamlandığı anlamına gelir. Frekans matematiksel olarak f simgesiyle gösterilir, birimi s-1 yani 1/s (1 bölü saniyedir). 1/s birimine özel bir isim verilir, Hertz (Hz) denir.
Periyot ile frekans arasındaki ilişki şöyledir:
T \times f = 1
Yani periyot ile frekansın çarpımı bire eşittir. Buradan frekansı:
f = \frac{1}{T}
olarak tanımlayabiliriz.
Yukarıdaki dönen üç cismin periyotlarını biliyoruz, bu nedenle frekanslarını da hesaplayabiliriz:
Yeşil cismin frekansı:
f_{yesil} = \frac{1}{4 \space s} = 0,25 s^{-1}
Yani bir saniyede 1/4 tur atıyor.
Turuncu cismin frekansı:
f_{turuncu} = \frac{1}{2 \space s} = 0,5 s^{-1}
Yani bir saniyede yarım tur atıyor.
Kırmızı cismin frekansı:
f_{kirmizi} = \frac{1}{1 \space s} = 1 s^{-1}
Yani bir saniyede bir tur atıyor.
Frekans arttıkça cismin daha hızlı döndüğünü fark etmelisiniz. Periyotta tam tersi oluyordu, periyot azaldıkça cisim daha hızlı dönüyordu.
Frekansı anlatmanın bir yolu da dakikada devir sayısı (rpm – revolutions per minute) kavramıdır. Motorların ne kadar hızlı döndüğünü anlatmak için frekans anlamında bir dakikada kaç devir yaptığı söylenir.
Açısal Hız nedir?
Açısal hızın ne olduğunu anlamak için önce açı ne demek onu anlamamız lazım. Kolay gibi gelebilir ama bir düşünün: Açı taranan alan mıdır yoksa uzunluk mudur? Açının birimi nedir?
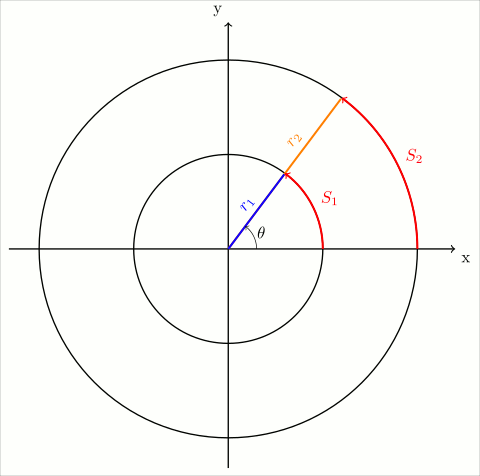
Yukarıdaki resimde iki çember görülüyor. İlk çember küçük olan, yarıçapı r1; ikincisi büyük olanı yarıçapı r2. Her iki çember için merkezle çemberin üstünde bir noktayı birleştiren birer çizgi çekilmiş, uzunlukları çemberlerin yarıçaplarına eşit. x -ekseniyle r1 arasındaki açı Θ, x – ekseniyle r2 arasındaki açı da Θ. Yani çember büyüse de açı değişmiyor. Öyleyse açı yarıçapın kendisiyle ilgili değil. Çemberlerdeki yay uzunluklarına da bakarsak S2 yayı S1 yayından daha uzun, eşit değiller, öyleyse açı yay uzunluğunun kendisiyle de ilgili değil. Alanla da ilgisi olamaz çünkü küçük çemberde Θ açısının taradığı alan, büyük çemberdekinden daha az. Peki bu iki çemberde birbirine eşit olan ne olabilir? Açı x-eseniyle yarıçapın arasındaki açıklık veya x-ekseninin yarıçapa kadar dönme miktarını anlatan bir kavram olmalı. Öyleyse:
Yay uzunluğunun yarıçapa oranı, açı olarak tanımlanabilir. Aslında açı tam olarak bu demektir. Bir de döndürme yönüne dikkat etmelisiniz, bir ışını saat yönünde ya da saat yönünün tersine doğru döndürebiliriz.
\theta=\frac{S}{r}=\frac{S_1}{r_1}=\frac{S_2}{r_2}Yay uzunluğunun birimi m, yarıçapın birimi de m. Bölme işleminde birimler sadeleşiyor. İşte bu nedenle, açının birimi yoktur, sadece saf sayıdır. Açının birimi yoksa radyan, derece, grad hatta milyem diye açı birimleri nereden çıkıyor?
Çemberin çevresinin uzunluğunun yarıçapa oranı tam açıyı tanımlamak için kullanılabilir. Bu orana 2π radyan, 360 derece, 400 grad veya 6400 milyem diyebilirsiniz. Hala radyan da, derece de, grad da, milyem de gerçek bir fiziksel birim olmaz. Bir oranı daha küçük parçalara bölmek için kullanılan bir numara olur sadece. Bir de dönme ile uğraştığımızı anlamamızı kolaylaştırmak için bu birimler kullanılır.
\theta=\frac{2\pi \cancel{r} \space radyan}{\cancel{r}}=\frac{360^\circ \cancel{r}}{\cancel{r}}Artık açısal hızı tanımlayabiliriz. Birim zamandaki açı değişimine açısal hız denir. Yani taranan açının zaman değişimine oranıdır. Açısal hız ω sembolüyle gösterilir. Açısal hızın fomülü de:
\omega = \frac{\Delta{\theta}}{\Delta{t}}Periyodu ya da frekansı biliyorsak açısal hızı da bulabiliriz. Yarıçapı bilmemize ihtiyacımız yok.
Çemberin çevresinin 2πr olduğunu biliyoruz. Bir tam tur çemberin 2π açı taraması anlamına gelir, bu kadar açıyı bir periyotluk sürede tamamladığına göre:
\omega = \frac{2\pi}{T}
T = \frac{1}{f}
\omega = \frac{2\pi}{\frac{1}{f}} = 2\pi f
Açısal hızın birimi 1/s gibi görünüyor ve öyle aslında. Ama açıdan bahsettiğimizi belirtmek için radyan/saniye birimini kullanırız. Açısal hızın \omega = 2\pi f ile frekansla olan bağlantısını ve frekansın birimiyle aynı birime sahip olması nedeniyle açısal hıza açısal frekans da dendiği olur.
Açısal hızın önemli bir özelliği de vektör olmasıdır. Açısal hız vektörel bir büyüklüktür. Dönme hareketinin bir yönü var. Bir cisim saat yönünde ya da saat yönünün tersine doğru dönebilir. Açısal hız vektörünün yönü dönüş yönünü gösterir. Dönen cisimlerin açısal hız vektörlerinin yönü sağ el kuralına göre bulunur.
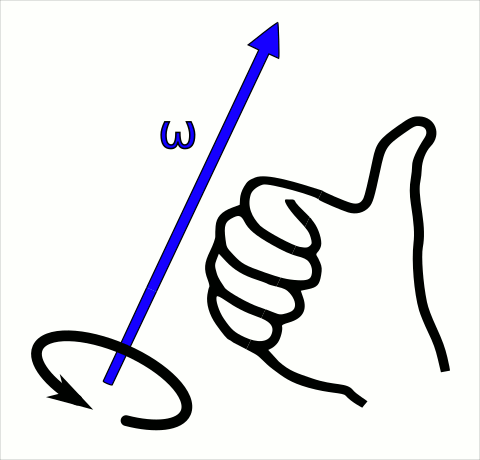
Saat yönünün tersine dönen bir cismin açısal hızını bulmak için, sağ elinizin dört parmağını dönen cismin hareket yönünü gösterecek şekilde kıvırırsınız, baş parmağınız açısal hız vektörünün yönünü gösterir. Yukarıdaki resimde açısal hız vektörünün yönü yukarı doğru.

Saat yönüde dönen bir cismin açısal hızını bulmak için, sağ elinizin dört parmağını dönen cismin hareket yönünü gösterecek şekilde kıvırırsınız,( bu durumda elinizi ters çevirmeniz gerekir) baş parmağınız açısal hız vektörünün yönünü gösterir. Yukarıdaki resimde açısal hız vektörünün yönü aşağı doğru. Açısal hız vektörünün şiddetine de açısal sürat denir.
Çizgisel sürat ile Açısal hız arasındaki ilişki nedir?
Çizgisel sürat, yani çizgisel hızın büyüklüğü (bu ayrıma çok dikkat etmelisiniz), bir hareketlinin aldığı yolun geçen süreye oranıdır. Düzgün çembersel hareket yapan bir cisim bir turda çemberin çevresi kadar yani S = 2πr kadar yol alır. Bir turu tamamlama süresine de periyot demiştik. Öyleyse çizgisel sürat:
v = \frac{2\pi r}{T}olur.
w = \frac{2\pi }{T}olduğunu biliyoruz. Öyleyse açısal hız ile çizgisel sürat arasındaki ilişki:
v =(\frac{2\pi }{T})r=\omega rolur.
Yani aynı açısal hızda düzgün çembersel hareket yapan bir cisim daha büyük bir yarıçapa çıkarsa çizgisel sürati (çizgisel hızının büyüklüğü) artmak zorundadır. Aşağıdaki resimde r ve 2r yarıçaplı çemberlerde sat yönünün tersine doğru düzgün çembersel hareket yapan iki cisim görülüyor. İç çemberdeki cismin sürati v iken, dış çemberdekinin sürati 2v, çünkü açısal hızları aynı ama dış çemberin yarıçapı iç çemberinkinin iki katı.
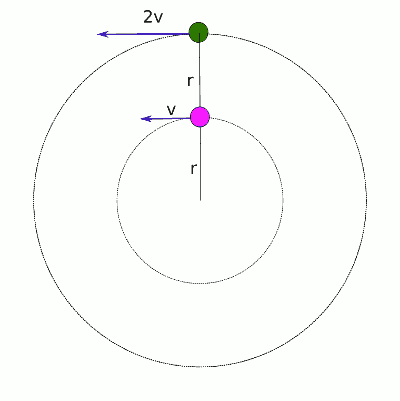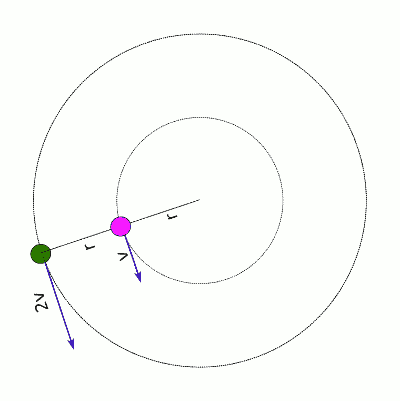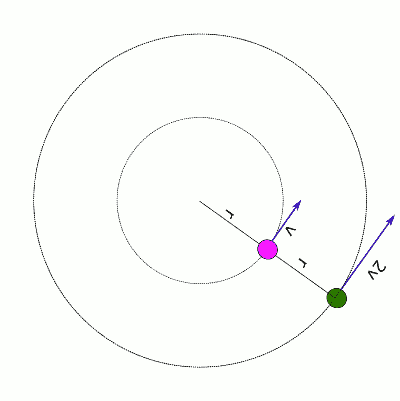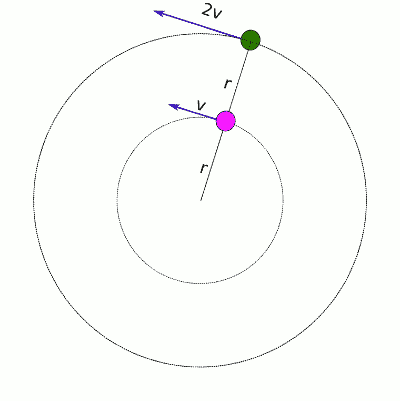
İç çemberdeki hareketli için (pembe cisim) v = ωr
Dış çemberdeki hareketli için çizgisel sürat: 2v = ω(2r)
Dış çemberdeki yeşil cismin aynı sürede pembe cisme göre iki kat yol alması gerekiyor.
Açısal hızın aynı olmasının periyot ve frekansından aynı olması anlamına geldiğini fark etmelisiniz. Hatırlayalım:
\omega=2\pi f = \frac{2\pi}{T}Israrla çizgisel sürat dediğimize dikkat edin. Çizgisel hız vektörünün yönü düzgün çembersel harekette sürekli değişiyor. Yukarıdaki resimdeki cisimlerin çizgisel hızları mavi oklarla gösteriliyor ve cisim döndükçe oklar da dönüyor. Ama okların uzunlukları yani sürat sabit.
Merkezcil ivme nedir? Çizgisel hız vektörünün değişimi
Düzgün çembersel harekette çizgisel süratin yani çizgisel hız vektörünün büyüklüğünün değişmediğini belirtmiştik. Ama bu çizgisel hız vektörün yönünün değişmediği anlamına gelmiyor. Cisim döndüğü için hareketin dolayısıyla hızın yönü sürekli değişiyor. Eğer zamana göre hız değişiyorsa ivme var demektir. İvmenin tanımını hatırlayalım:
\vec{a} = \frac{\vec{\Delta v}}{\Delta t} = \frac{\vec{v_2}-\vec{v_1}}{t_2 - t_1}Şimdi küçük bir zaman aralığı için (0,01 saniye diyebiliriz örneğin) düzgün çembersel hareket yapan bir cismin hız vektöründeki değişimi görsel olarak inceleyelim.
- İvmeyi bulmak için bir ilk konum bir de son konum seçiyoruz.
- İlk ve son konumlardaki hızlara sırasıyla v1 ve v2 diyoruz.
- Son hızdan ilk hızı vektörel olarak çıkarmamız gerekiyor. v2 – v1 = v2 + (-v1) olduğu için v1 vektörünü ters çeviriyoruz.
- v2 vektörüyle -v1vektörünü uç uca ekleyerek topluyoruz.
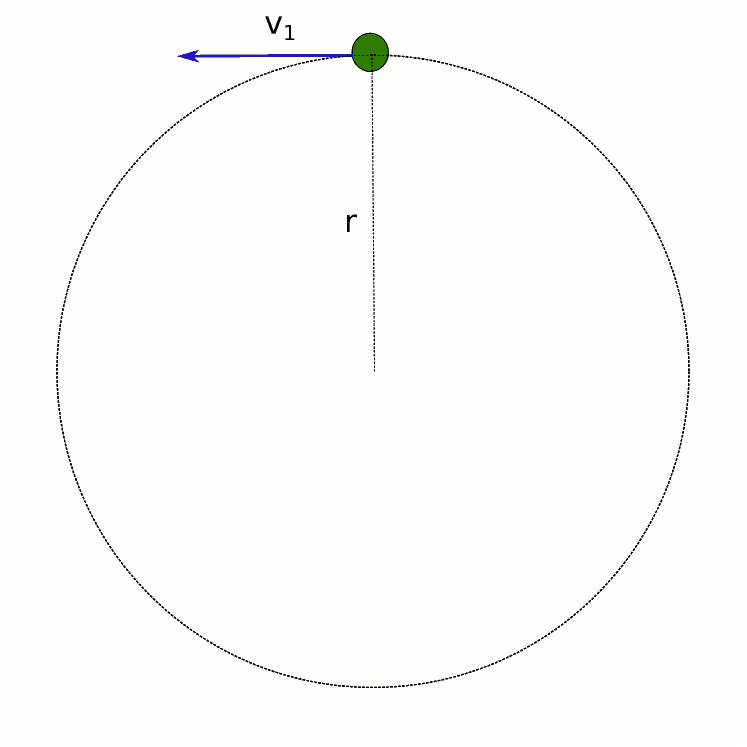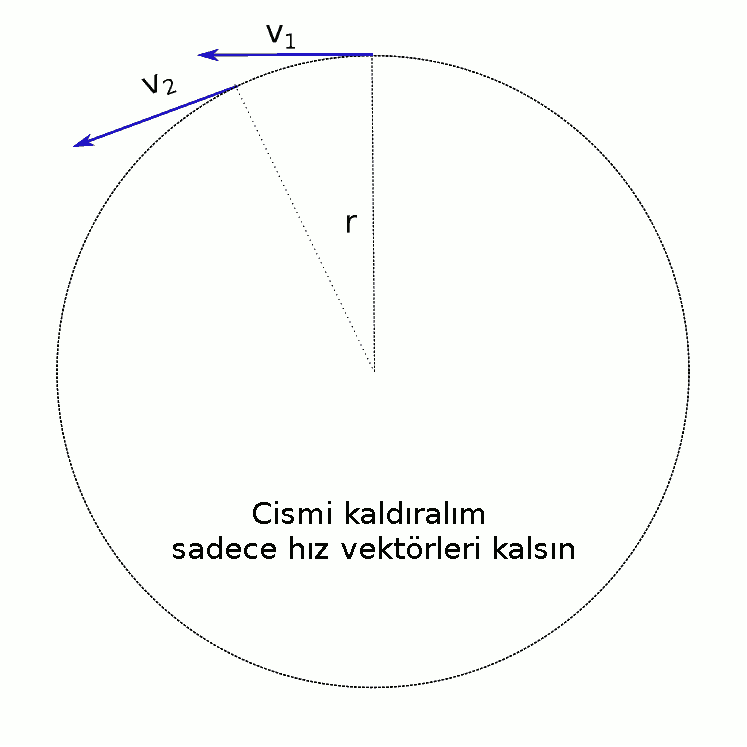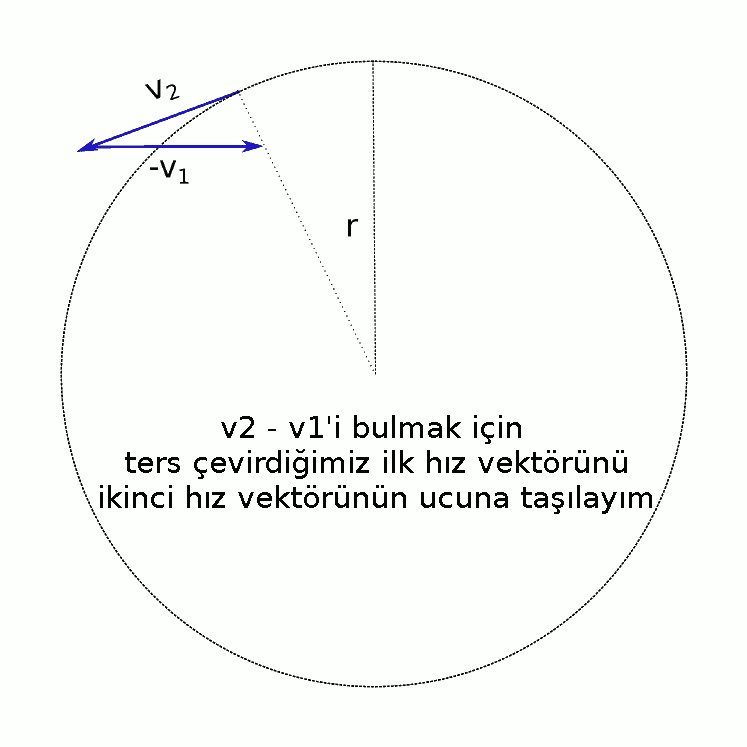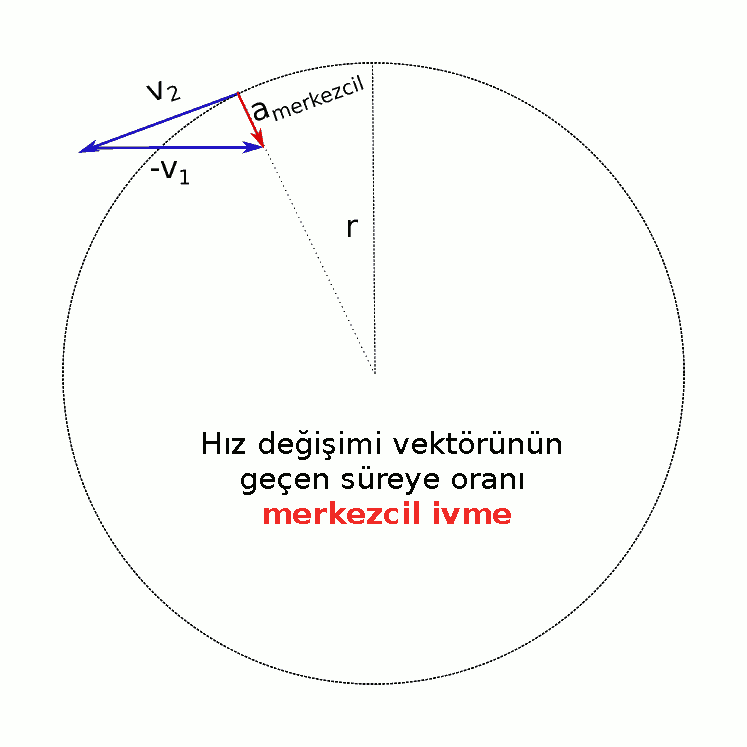
- Fark vektörü \vec{v_2} - \vec{v_1} kırmızıyla gösteriliyor.
- Fark vektörünün zaman aralığına oranı ivmeyi veriyor:
\vec{a} = \frac{\vec{v_2} - \vec{v_1}}{t_2 - t1} - İvmenin yönü çok önemli. Her zaman çemberin merkezine doğru. İşte bu nedenle düzgün çembersel harekette ivmeye merkezcil ivme deniyor. Ayrıca merkezcil ivme vektörünün yönü daima çizgisel hız vektörünün yönüne dik. Çünkü çizgisel hız çembere her noktada teğetken, merkezcil ivme hep merkeze doğru. Çembere çizilen bir teğet her zaman yarıçapa diktir. (Geometri önemli.)
Merkezcil ivmenin yönünü bulduk ama büyüklüğünü nasıl bulacağız? Hareketli çemberin etrafında bir tam tur attığında hız vektöründeki toplam değişim 2πv olur. Geçen süre de periyoda eşit olur. Öyleyse ivmenin tanımından:
\vec{a} = \frac{2\pi v}{T}Çemberin çevresinin çizgisel sürate oranı periyodu verir:
T = \frac{2\pi r}{v}Periyodu ivme denklemine yerleştirirsek:
\vec{a} = \frac{2\pi v}{\frac{2\pi r}{v}} = \frac{v^2}{r}buluruz. Merkezcil ivmenin formülü çok önemli hatırlamalısınız.
Düzgün Çembersel Hareket Örnek Sorular ve Çözümleri
Soru 1: Çembersel Pistteki Yarış Arabasının Açısal Hızı
Yarıçapı 1 km olan çembersel bir pistte 120 km/h sabit süratle hareket eden bir yarış arabasının periyodu, frekansı ve açısal hızı ne kadardır?
Çözüm:
Periyot bir tam tur atana kadar geçen süre demektir. Çemberin çevresini ve arabanın süratini bildiğimiz için periyodu da bulabiliriz.
Çemberin çevresi = 2πr = 2. 3,14 . 1000 m = 6280 m (km’yi metreye dönüştürüyoruz.)
Arabanın süratini de km/h biriminden m/s birimine dönüştürelim:
v=120\frac{km}{h}\times \frac{1000m}{1km} \times \frac{1h}{3600s}v = 33,3 m/s bulduk. Birim dönüşümünde birbirini götüren km ve m ile h ve s birimlerine dikkat edin.
Şimdi periyodun tanımından:
T=\frac{2\pi r}{v}=\frac{6280 m}{33,3 m/s} = 188,6 sPeriyodu bildiğimize göre frekansı bulmak da kolay, frekansın tanımından:
f=\frac{1}{T}=\frac{1}{188,6s} = 0,005 s^{-1}Son olarak açısal hızı bulalım. Frekansı bildiğimiz için açısal hızın tanımından:
\omega=2\pi f = 2 \times 3,14 \times 0,005 = 0,03 rad/sAçısal hızın birimini rad/s olarak belirttik.
Soru 2: Çizgisel hız bilinirken frekans oranı
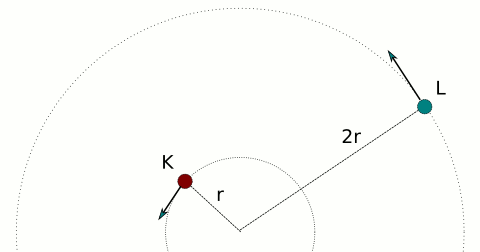
Yukarıdaki şekilde gösterilen K cismi v, L cismi 6v çizgisel süratiyle düzgün dairesel hareket yapmaktadır. K cisminin frekansı f olduğuna göre L cisminin frekansı kaç f dir?
Çözüm:
K cisminin frekansının f, çizgisel hızının büyüklüğünün v olduğunu biliyoruz. Çizgisel sürat ile frekans arasındaki ilişki, açısal hızla frekans arasındaki ilişkiden geçiyor.
v = ωr
ω = 2πf
f = ω/2π
2π sabit olduğu için çizgisel hız ile frekans doğru orantılı.
v = 2πfr
f = v/2πr
L cisminin hızı ile frekansı arasındaki ilişkiyi yazalım:
6v = 2πfL3r (r + 2r = 3r dikkat edin!)
fL = 6v/6πr = v/πr
Frekansları oranlarsak:
\frac{f_L}{f} = \frac{\frac{v}{2\pi r}}{\frac{v}{\pi r}} = 2
Yani fL = 2f bulduk.
Peki K mı L mi daha hızlı dönüyor? Düşünün.
Soru 3: Kızağın merkezcil ivmesi
Yarıçapı 150 m olan dairesel bir pistte sabit süratle yol alan bir kızak bir turu 60 saniyede tamamlamaktadır.
Buna göre kızağın merkezcil ivmesi kaç m/s2 dir? (π=3 alın.)
Çözüm:
Önce merkezcil ivmenin tanımını yazalım:
\vec{a}_{merkezcil}=\frac{v^2}{r}
Öyleyse hızı (sürati) bulmalıyız. Çemberin çevresinin periyoda bölümü:
v=\frac{2\pi r}{T}
v=\frac{2\times 3 \times 150 m}{60 s}
v= 15 m/s bulduk. İvme denkleminde yerine yerleştirelim:
\vec{a}_{merkezcil}=\frac{15^2}{150}=1,5 m/s^2
Düzgün Çembersel Hareket ile ilgili Simülasyon
İki boyutta uğur böceğinin hareketi PHET simülasyonunun Türkçesinde düzgün çembersel hareketi keşfedebilirsiniz.
Düzgün Çembersel Hareket ile ilgili Kazanımlar
Düzgün çembersel hareketi açıklar.
- Periyot, frekans, çizgisel hız ve açısal hız, merkezcil ivme kavramları verilir.
- Öğrencilerin düzgün çembersel harekette çizgisel hız vektörünü çember üzerinde iki farklı noktada çizerek merkezcil ivmenin şiddetini bulmaları ve yönünü göstermeleri sağlanır. Çizgisel ivme kavramına girilmez.
Açısal sürat için yazılmış tüm formüller dönüş yapan katı bir cisim içinde geçerlidir. Bu bölümde dönüş yapan sabit cismin bir eksen üzerinde dönmediği kabul edilmiştir. Bu bölümde sabit cismin, rastgele seçilmiş V(t) ile hareket eden bir noktaya göre dönüş yaptığı düşünülmüştür.
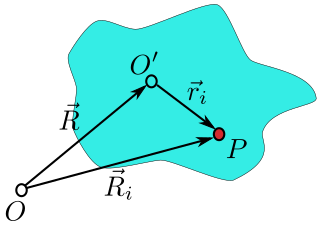
Denklemleri oluşturabilmek için katı cismin koordinat sisteminde bir noktaya göre sabit tutulduğu varsayılır, daha sonra bu koordinat düzlemi ve katı cisim arasındaki alan laboratuvar sisteminde incelenir. Resimde görüldüğü gibi laboratuvar sisteminin merkezi O noktasından O' noktasına kadar R’dir. Bir (i) parçacığı katı cisim üzerinde belirlenmiştir ve P noktası üzerinde olduğu kabul edilmiştir ve bu parçacığın vektör durumu Ri olarak alınmıştır (laboratuvar sistemi) ve (ri ) cisime göre alınmıştır. Parçacığın bulunduğu yer şe şekilde ifade edilebilir; 

















