Pisagor Ispatı Sulu

pisagor ispatı sulu

Pisagor Teoreminin Origami ile İspatı

If you're seeing this message, it means we're having trouble loading external resources on our website.

Bağlandığınız bilgisayar bir web filtresi kullanıyorsa, *.kastatic.org ve *.kasandbox.org adreslerinin engellerini kaldırmayı unutmayın.

Ödevinizi yorum kısmına yazın. Açıklık ve özlülük ek puan getirir! Bu video için birlikte fikir ürettiğimiz New York Üniversitesi'nden arkadaşlarıma özellikle teşekkür ederim.Orijinal video Vi Hart tarafından hazırlanmıştır.

Video açıklaması

Pisagor teoremini kanıtlamak için sayılara veya süslü denklemlere ihtiyacınız yok. Tek ihtiyacınız bir kağıt parçası. Bunu kanıtlamak için bir sürü yol var ve insanlar sürekli bir yenisini icat ediyorlar. Ama ben size favorimi göstereceğim. Sadece diyagramlara bakmak yerine, katlayacağız. Önce bir kareye ihtiyacımız var. Bir dikdörtgene nazikçe sorarsanız belki kare olmayı kabul edebilir. birinci adım; karenizi ortadan ikiye katlayın, sonra öbür yöne ikiye, sonra da köşegenden ikiye. Kat yerlerinin keskin olmasına gerek yok, ikinci adımda karenin simetrilerini kullanacağız o kadar: Ama siz yine de dikkatli olun Üçgenin açık uçlarının olduğu kenara paralel bir kat yapın istediğiniz yerden katlayabilirsiniz. Burada dik üçgeninizin ne kada uzun ve dik veya kısa ve büük olduğuna siz karar veriyorsunuz. Tüm katları geri açtığınızda, karenizin içinde bir kare daha olduğunu göreceksiniz. Bu katları biraz daha keskinleştirin ve şimdi kenarlara eşit uzaklıkta dört çizgimiz olmalı Bakalım buradan kaç tane özdeş dik üçgen yapabileceğiz. aslında dikdörtgenin köşegenini almış oluyoruz. Böylece ilk dik üçgenimizi tamamladık. bununla aynı şekle ve aynı alana sahip. Üçgenimizin kenarlarını Küçük kenar, büyük kenar ve hipotenüs olarak isimlendirelim Doksan derece döndürelim ve öbür üçgeni katlayalım. Bu da tabii ki ilki gibi yapalım Sonraki iki kenar için de tekrar edelim Orijinal kağıt eksi bu dört üçgen, bize bu güzel kareyi veriyor. Bu kağıdın alanı ne kadar? Karenin kenarları aslında bu üçgenlerden herhangi birinin hipotenüsü. Yani alan aslında hipotenüsün karesi oluyor. katladıklarınızı açın ve bu sefer katlamak için dört farklı üçgen seçin. Küçük kenardan yırtın ve bu iki üçgeni geri katlayın. Sonra buradan iki tane katlayabilirsiniz. hangi dört üçgeni çıkarırsanız çıkarın. Katlanmamış alandan dört üçgeni çıkarttığınızda alan aynı olmalı. şimdi bakalım elimizde ne var? Bunu iki kareye bölebiliriz. Bunun kenarları üçgenin kısa kenarı. Bunun kenarları da üçgenin uzun kenarı kadar. Yani ikisinin toplam alanı, küçük kenarın karesi ve büyük kenarın karesi. Bu da buranın alanına eşit olmak zorunda, yani hipotenüsün karesi. Eğer üçgenin kenarlarına daha soyut isimler verseydiniz, örneğin: a, b ve c. Elinizdeki kağıda baktığınızda. a kare artı b kare eşittir c kare olurdu. Kısaca bir tekrar edelim. Adım bir: Üç kere ikiye katlayın. Adım iki, istediğiniz bir yerden kenarlara paralel katlayın ve kat izini keskinleştirin. Adım üç, karenin çevresinde dört dik üçgen katlayın ve kalan alanın hipotenüsün karesi olan kalan alanı fark edin. Katları açın ve kısa yerden yırtın sonra farklı dik üçgen katlayın. Kalan alanın bir kenarın karesi artı diğer kenarın karesi olduğunu göreceksiniz. İşte hepsi bu. Tabii ki, matematikçiler isyankardır, ve başkalarının onlara söyledikleri şeylere inanmazlar, Yani ben size şunun gibi şeyler söylediğimde inanmayın: Bu bir kare. Kendinizi ikna edebileceğiniz yolları düşünün üçgenlerin dışarıdan nasıl göründüğü fark etmez, Çünkü sonuçta bu hep bir kare olacaktır. bir eşkenar dörtgen paralel kenar veya bir yunus değil. yada belki bir yunustur ve bunu sadece siz biliyorsunuzdur.

Pisagor teoremi geometride en fazla kullanılan teoremlerden biridir. Bu teorem her ne kadar antik Yunan filozoflarından Pisagor ile özdeşleştirilse de hala bu teoremin ilk olarak kim tarafından ispatlandığı tartışma konusudur. Pisagor'dan çok önceki tarihlerde Babil, Hint, Çin, Mısır ve Mezopotamya'da bulunan kayıtlarda bu teoremin kullanıldığı ve bazı özel durumlar için ispatlandığı görülmüştür. Teorem geçmişten günümüze farklı yöntemler ile sayısız kere ispat edilmiştir. Bu makalemde Pisagor teoreminin en basit iki ispat yönteminden bahsetmek istiyorum.

Şu konuya da değinmeden geçemeyeceğim; çoğu kişi bu teoremi "bir dik üçgende hipotenüsün karesi, diğer kenarların karelerinin toplamına eşittir" olarak bilse de, teoremin bir başka tanımı da "birbirinden farklı üç kare, bir dik üçgen oluşturacak şekilde bir araya gelebiliyorsa, büyük karenin alanı, diğer karelerin alanlarının toplamına eşittir" şeklindedir. Konu sonundaki videoda bu tanımın deneyini izleyebilirsiniz.

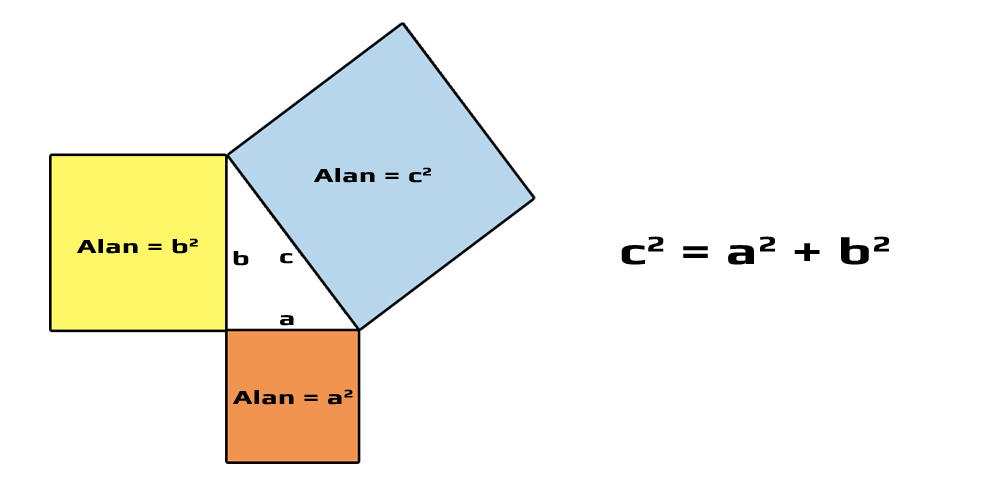
1 - Pisagor'un İspatı

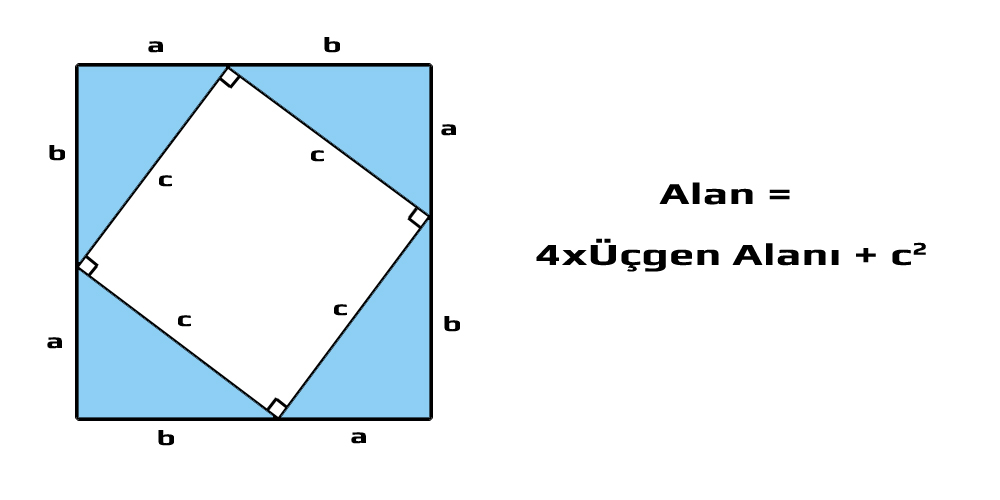
Pisagor'un ispat yöntemine "yeniden düzenleme" adı verilmiş ve farklı teorem ispatlarında kullanılmıştır. Pisagor birbirinin aynısı 4 dik üçgen oluşturmuş ve bu üçgenleri birleştirerek aşağıdaki resimde görülen şekli elde etmiştir. Resimdeki a + b kenarlı büyük karenin alanı, 4 üçgen alanı ve c kenarlı küçük karenin alanlarının toplamına eşittir. Yani büyük karenin alanı, 4 üçgen alanı + c² 'dir.

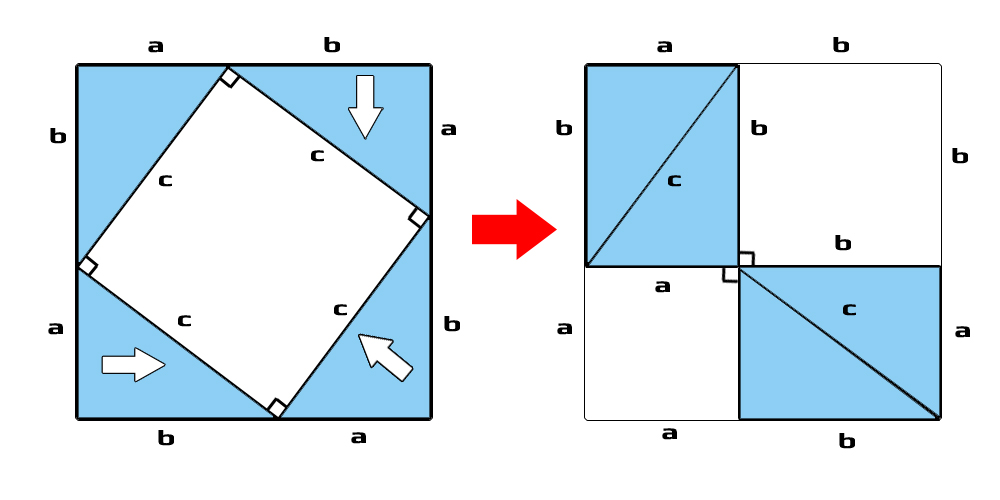
Üçgenleri aşağıdaki resimdeki gibi ok yönlerinde hareket ettirdiğimizde aynı alana sahip, farklı bir şekil elde ederiz. Oluşan yeni şekil, 2 küçük kare ve 4 üçgenden oluşmaktadır.

Yeni düzenleme ile a + b kenarlı karenin alanı, 4 üçgen alanı ile 2 küçük karenin alanlarının toplamına eşittir.

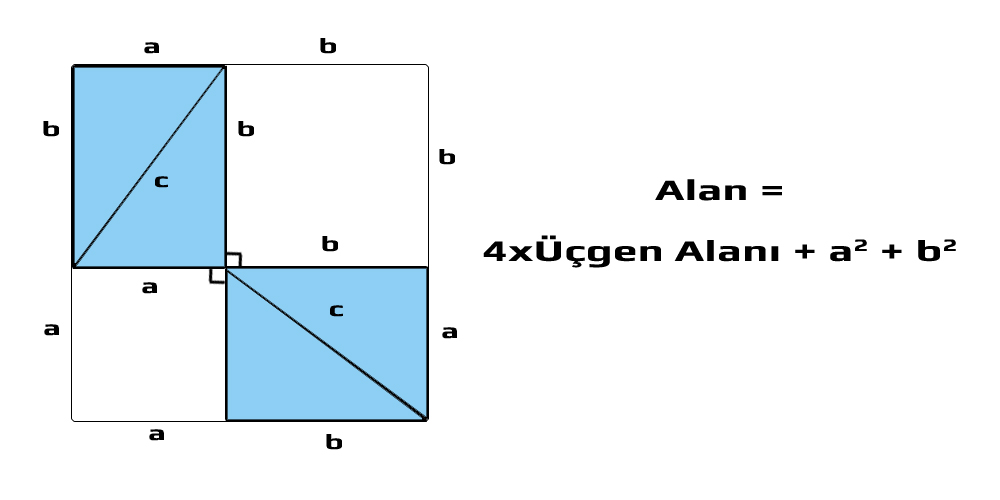
Böylece büyük karenin alanını iki farklı formül ile ifade edebildik. Bu formüller birbirine eşit olduğundan

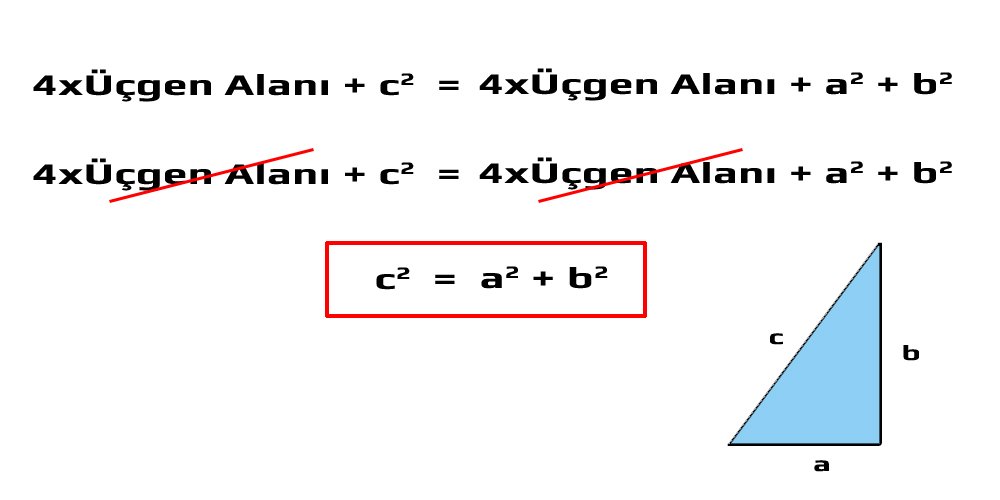
Aşağıdaki Pisagor'un yeniden düzenleme yönteminin anlatıldığı videoyu izleyebilirsiniz.

2 - Üçgen Benzerliği İspatı

Bir dik üçgende, dik kenardan hipotenüse bir dikme indirildiğinde birbirine benzer üç üçgen elde edilir. Üçgenler arasındaki benzerlik oranları yazılırsa,

bağıntıları oluşturulur. Bağıntılar matematiksel olarak içler dışlar çarpımı yapılıp toplanırsa,

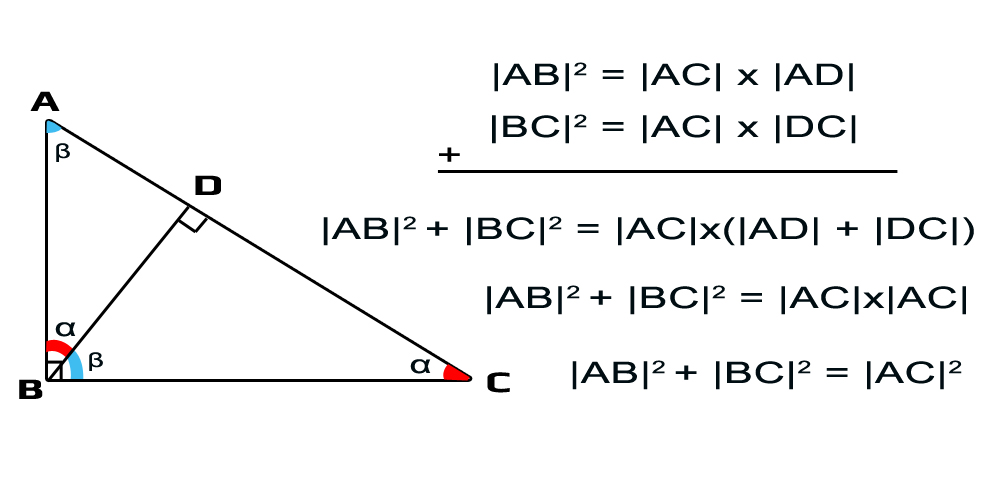
eşitliği bulunur. Böylece pisagor bağıntısını iki basit yöntem ile ispatlamış oluyoruz. Aşağıdaki videoda Pisagor teoreminin ispatı için yapılmış su deneyini görebilirsiniz.

Pisagor teoremi

Pisagor teoremi
Bacaklar (a ve b) iki karenin alanlarının toplamı, karenin hipotenüs (c) üzerindeki alanına eşittir

Pisagor teoremi (Yunanca: Πυθαγόρειο θεώρημα) veya Pisagor bağıntısı, Öklid geometrisinde üçgenin kenarları arasındaki temel ilişkiyi kuran ilk teoremlerden biridir. Teoreme gerçek hayattan örnek olarak telli çalgıları gösterilebilir; 'telin uzunluğu arttıkça titreşim artar' prensibine dayanır. Pisagor'un denklemi olarak da isimlendirilen bu teorem, a, b ve c kenarlarının arasındaki ilişkiyi şu şekilde açıklar:^[1]

$a^{2}+b^{2}=c^{2},$

burada c hipotenüsün uzunluğunu, a ve b üçgenin diğer iki tarafının uzunluklarını temsil eder. Tarihî anlamda çok tartışılan teorem, adını eski Yunan filozof ve matematikçi Pythagoras'dan ‪(Πυθαγόρας, MÖ 570 – MÖ 495) almıştır.

Bu teorem, birçok matematiksel teoremin ispatlanmasını sağlamıştır. Binlerce yıl öncesine dayanan geometrik ispatlar ve cebirsel ispatlar da dahil olmak üzere bu, çok çeşitlidir. Bu teorem, yüksek boyutlu uzaylardan, Öklid olmayan uzaylara, doğru üçgen olmayan nesnelere ve aslında hiç üçgen olmayan nesnelere, n boyutlu katılara çeşitli şekillerle entegre edilip genelleştirilebilir. Pisagor teoremi, matematiksel soyutlamanın, mistik ya da entelektüel gücün sembolü olarak matematiğin ilgisini çekmiştir; edebiyat, sinema, müzikal, şarkı ve çizgi filmlerde de popüler olmuştur.

Yeniden düzenleme ispatı[değiştir kaynağı değiştir]

^Judith D. Sally; Paul Sally (2007). "Chapter 3: Pythagorean triples". Roots to research: a vertical development of mathematical problems. American Mathematical Society Bookstore. s. 63. ISBN 0-8218-4403-2. 19 Ağustos 2020 tarihinde kaynağından arşivlendi. Erişim tarihi: 16 Mayıs 2020.
^Benson, Donald. The Moment of Proof : Mathematical Epiphanies 18 Ağustos 2020 tarihinde Wayback Machine sitesinde arşivlendi., pp. 172–173 (Oxford University Press, 1999).
^Euclid (1956), pp. 351–352
^Huffman, Carl. "Pythagoras". Zalta, Edward N. (Ed.). The Stanford Encyclopedia of Philosophy (Winter 2018 Edition). 8 Mart 2021 tarihinde kaynağından arşivlendi. Erişim tarihi: 25 Ağustos 2020. , "It should now be clear that decisions about sources are crucial in addressing the question of whether Pythagoras was a mathematician and scientist. The view of Pythagoras' cosmos sketched in the first five paragraphs of this section, according to which he was neither a mathematician nor a scientist, remains the consensus."
^Loomis 1968

nest...

230785 230786 230787 230788 230789